Nesse capítulo vamos fazer as pazes com matemática. Vamos concordar que matemática
é uma ciência azeda e árida, porém é a ciência cujo domínio permite fazer coisas
geniais em programação de jogos. O limite dos seus jogos vai refletir o limite
que você tem em matemática.
As mesmas coisas podemos dizer de física e geometria, porém o conhecimento de
matemática é preponderante e perpassa essas matérias. No final de contas,
o que você vai precisar compreender de física e geometria são as relações
matemáticas das variáveis e grandezas envolvidas.
Neste capítulo vamos apenas explorar superficialmente os poderes gráficos da
trigonometria que nos permite movimentar objetos numa trajetória circular,
angular ou elíptica.
Veja nosso programa exemplo, e depois vamos explicar a equação chave que produziu
os efeitos gráficos da imagem acima.
//trigonometria.cpp
//Esse programa mostra como usar as funções de trigonometria para desenhar círculos
//e elipses
#include "DarkGDK.h"
// Protótipo das funções
void initsys(); // inicializa o sistema
void trigonometria(void); // Desenha circulos e elipses
int sorteia_cor(); // Sorteia uma cor aleatória
// Cores
const int nPreto = 0;
const int nBranco = 0xFFFFFF;
const int nAzul = 0x0000FF;
// ----------------------------------------------------------------------------
void DarkGDK ( void ) {
// Começo da aplicação DarkGdk
initsys();
while ( LoopGDK ( ) ) {
trigonometria();
dbSync ( );
} // fim do while
return;
} // fim da função: DarkGDK
// ----------------------------------------------------------------------------
void initsys() {
// Esta função inicializa o sistema
dbSyncOn( ); dbSyncRate (60);
dbCLS(nBranco);
dbSetWindowTitle("trigonometria.cpp");
dbSetTextOpaque();
dbRandomize( dbTimer() );
} // fim da função: initsys()
// ----------------------------------------------------------------------------
void trigonometria(void) {
//Centro do círculo e da elipse
int xpos,ypos;
//Propriedades do ponto a ser desenhado
float xraio,yraio,angulo;
//Ponto final na tela da extremidade do circulo
int sx,sy;
//Ponto final na tela da extremidade da elipse
int dx,dy;
xpos=210;ypos=220;
for(angulo=0;angulo<=360;angulo+=10)
{
dbInk ( sorteia_cor(), nAzul);
// Desenha circulo ao redor do olho
xraio = 180; yraio = 180;
sx = xpos + (xraio * dbCos(angulo) );
sy = ypos + (yraio * dbSin(angulo) );
dbCircle (sx, sy, 10); dbCircle (sx, sy, 9); dbCircle (sx, sy, 8);
// Desenha elipse do olho
xraio = 180; yraio = 90;
dx = xpos + (xraio * dbCos(angulo) );
dy = ypos + (yraio * dbSin(angulo) );
dbCircle (dx, dy, 10); dbCircle (dx, dy, 9); dbCircle (dx, dy, 8);
// Desenha a pupila
xraio = 60; yraio = 60;
sx = xpos + (xraio * dbCos(angulo) );
sy = ypos + (yraio * dbSin(angulo) );
dbCircle (sx, sy, 10); dbCircle (sx, sy, 9); dbCircle (sx, sy, 8);
dbLine(sx,sy, dx,dy);
// Mostre o angulo na tela
dbInk (nBranco, nAzul);
dbText (10,10, dbSpaces(20));
dbText (10,10, "Angulo: "); dbText (100,10, dbStr (angulo));
// Mostre os gráficos e espere um pouco
dbSync(); dbSleep(100);
} // fim do for (angulo)
} // trigonometria().fim
int sorteia_cor() {
//Variáveis de trabalho com cor
int ncor,r,g,b;
//Gera uma cor aleatória
r=dbRnd(255);g=dbRnd(255);b=dbRnd(255);
ncor=dbRGB(r,g,b);
return ncor;
} // get_cor().fim
Explicando o movimento circular
// Desenha circulo ao redor do olho
xraio = 180; yraio = 180;
sx = xpos + (xraio * dbCos(angulo) );
sy = ypos + (yraio * dbSin(angulo) );
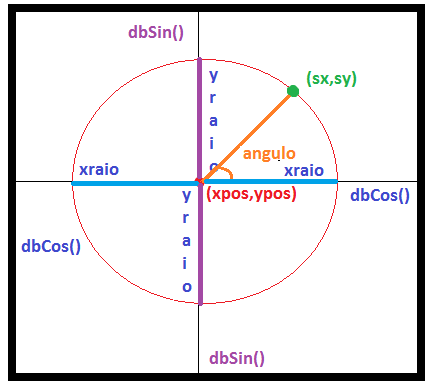
Primeiro lembramos que um circulo é conjunto de pontos (sx,sy) distantes
igualmente (raio) de um mesmo centro em comum (xpos,ypos).
Visualize em nosso diagrama que (xpos,ypos) é a posição a partir da qual o
ponto (sx,sy) é desenhado. A distância entre (sx,sy) e (xpos,ypos) é dada
por xraio (= 180) ou yraio (= 180).
(xraio * dbCos(angulo)) refere-se a distância horizontal, peculiar a cada
angulo, no eixo x do ponto (sx,sy).
(yraio * dbSin(angulo)) refere-se a distância vertical, peculiar a cada
angulo, no eixo y do ponto (sx,sy).
A variável angulo que passamos em dbCos() e dbSin() estabelece o angulo do
ponto no perímetro circular.
Em um círculo o raio horizontal (xraio) e o raio vertical (yraio) tem o
mesmo tamanho. A diferença de valores entre esses raios produz a elipse.
Mantenha em mente que o cosseno (dbCos()) refere-se aos pontos do eixo x,
e o seno (dbSin()) refere-se aos pontos no eixo y.
Movimento em uma direção angular
Em nosso programa exemplo usamos uma estrutura for(;;) para gerar diversos
angulos parar desenhar nosso círculo e o raio do circulo ficou imóvel sem
alterações.
Tem uma situação que é o inverso, por exemplo, no deslocamento de uma
bala de canhão, você vai fixar um angulo no qual a bala vai se deslocar e
você vai usar uma estrutura for(;;) para aumentar gradualmente o raio de
distância para mover a bala percorrendo a linha do ângulo determinado.